Coeficiente de utilización en alumbrado público: ¿por qué es importante?
Coeficiente de utilización en alumbrado público: ¿por qué es importante?
Introduction
Tras la emisión de luz de la lámpara, ¿cuánta luz puede alcanzar la superficie de trabajo? En el caso de las luminarias de interior, una parte de la luz emitida por una lámpara industrial llega directamente a la superficie de trabajo, mientras que otra parte incide en la pared y el techo, reflejándose en ella. El resto no alcanza la superficie de trabajo (por ejemplo, la luz sobre una estantería). El coeficiente de utilización es el flujo luminoso (¿qué es el flujo luminoso?) que llega a la superficie de trabajo dividido entre el flujo luminoso de la fuente de luz. En el alumbrado público, también se conoce como coeficiente de utilización, pero generalmente se presenta como una curva de coeficiente de utilización. En el alumbrado público, es necesario considerar la distribución de la luz emitida por la lámpara en ambas direcciones: la calle y la vivienda. Este artículo analiza principalmente el coeficiente de utilización, la curva del coeficiente de utilización, los parámetros que lo afectan, su importancia como guía y cómo podemos usar la curva del coeficiente de utilización para seleccionar mejor la distribución de la luz y la disposición de las lámparas en aplicaciones prácticas para obtener mejores resultados de iluminación. Analicemos el texto para obtener más información.
¿Qué es el coeficiente de utilización?
El coeficiente de utilización, también llamado factor de utilización, determina la eficiencia lumínica de una luminaria en una aplicación específica. Su fórmula de cálculo es la siguiente: Coeficiente de utilización = flujo luminoso proyectado sobre la superficie de trabajo / flujo luminoso total de la lámpara. Mide la eficiencia de la lámpara al transferir la energía luminosa a la superficie de trabajo en un área específica. En la iluminación interior, el factor de utilización se ve afectado por factores como la distribución espectral, el tamaño del espacio (índice de la sala) y la reflectividad de diversas superficies interiores (paredes, techos y suelos). Idealmente, el factor de utilización de las lámparas industriales y mineras para iluminación interior puede alcanzar 1 o incluso superarlo ligeramente; en la iluminación vial, el factor de utilización se relaciona con factores como las características espectrales, el ángulo de inclinación de la lámpara y la longitud del brazo, y suele presentarse como una curva de coeficiente de utilización. En la iluminación interior, se utiliza el método del lúmen para estimar aproximadamente el efecto luminoso (iluminancia) tras la instalación de la lámpara. Este método también se denomina método del factor de utilización, ya que utiliza dicho parámetro. Su fórmula de cálculo es: Eav (iluminancia media) = Φ (flujo luminoso de una lámpara) x N (número de lámparas) x CU (factor de utilización) x K (factor de mantenimiento) ÷ A (área). Para obtener más información, puede consultar el blog correspondiente de ZGSM: “Método de cálculo de lúmenes y sus beneficios“.
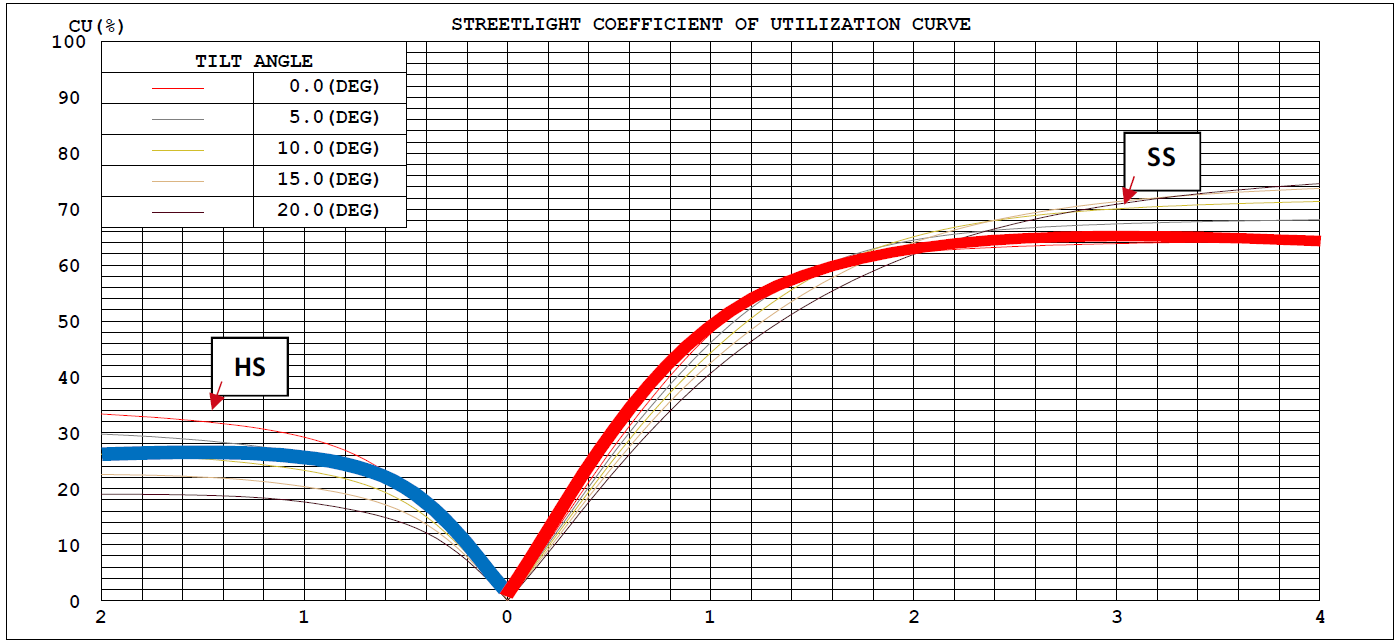
¿Qué afecta al coeficiente de utilización?
En cuanto al valor del coeficiente de utilización, podemos obtener información general del texto mencionado en la sección anterior. Tomando como ejemplo las luces industriales de interior, cuando la distribución de la luz es diferente, el tamaño del espacio es diferente y la reflectividad de la superficie de la habitación es diferente, el valor de CU también cambiará. La siguiente es la tabla del factor de utilización (también llamado coeficiente de utilización) de las luces de gran altura ZGSM Helios (Más sobre las luces de gran altura ZGSM Helios). Cuando la lente es diferente, el UF del ángulo de haz de 60 grados es 0.82 en k (índice de habitación) = 0.6 y ρc = 0.8, ρw = 0.8 y ρf = 0.2, mientras que el UF del ángulo de haz de 120 grados es solo 0.54. Porque cuanto mayor sea el ángulo de haz, más luz necesita pasar a través de la pared y el techo hasta el suelo (área objetivo). Cuando la lente es la misma (120 grados), la diferente reflectividad de la pared, el techo y el piso también afectará el valor del UF. Las diferencias se muestran en la tabla. Cuando la reflectividad y la habitación son iguales, cuanto menor sea el índice de la habitación (¿Qué es el índice de la habitación?), menor será el valor UF. Esto se debe a que cuanto menor sea el índice de la habitación, más pequeña será la habitación (o la habitación es larga y estrecha). En este momento, puede imaginar que una gran parte de la luz emitida por la lámpara brillará en las paredes circundantes, lo que conducirá a un valor UF menor. Entonces, en las farolas, ¿qué factores están relacionados con el UF (coeficiente de utilización)? ZGSM cree que está relacionado principalmente con la distribución de la luz, el ángulo de inclinación de la lámpara y la longitud del brazo. Vamos a explicarlos uno por uno a continuación.
| Beam angle 60 degree | ||||||||||
| REFLECTANCE | ||||||||||
| Ceiling | 0.8 | 0.8 | 0.8 | 0.7 | 0.7 | 0.7 | 0.5 | 0.5 | 0.5 | 0 |
| Walls | 0.7 | 0.5 | 0.3 | 0.7 | 0.5 | 0.3 | 0.7 | 0.5 | 0.3 | 0 |
| Working plane | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0 |
| ROOM INDEX | UTILIZATION FACTORS(PERCENT) k(RI) x RCR = 5 | |||||||||
| k = 0.60 | 82 | 75 | 70 | 81 | 74 | 70 | 80 | 74 | 70 | 66 |
| 0.8 | 90 | 83 | 79 | 89 | 83 | 79 | 88 | 82 | 78 | 74 |
| 1 | 95 | 89 | 85 | 95 | 89 | 85 | 93 | 89 | 84 | 80 |
| 1.25 | 100 | 94 | 90 | 99 | 94 | 90 | 97 | 92 | 89 | 84 |
| 1.5 | 103 | 98 | 94 | 102 | 97 | 93 | 100 | 95 | 92 | 87 |
| 2 | 107 | 102 | 98 | 105 | 101 | 97 | 102 | 99 | 96 | 90 |
| 2.5 | 109 | 104 | 101 | 107 | 103 | 100 | 104 | 101 | 98 | 92 |
| 3 | 110 | 107 | 103 | 109 | 105 | 102 | 105 | 102 | 100 | 94 |
| 4 | 113 | 110 | 107 | 111 | 108 | 106 | 107 | 105 | 103 | 96 |
| 5 | 114 | 111 | 109 | 112 | 110 | 108 | 108 | 106 | 105 | 97 |
| ROOM INDEX | UF(total) | Direct | ||||||||
| According to DIN EN 13032-2 2004 Suspended SHRNOM = 1.25 | ||||||||||
